Strong Entity Integrity: Part 4 — Join

In relational algebra, the join operator is defined as the Cartesian product (cross join) of two relations A and B followed by a restriction.

The unrestricted cross join constructs a new entity class as the combination of the two entity classes of its inputs.  Then the entity class of the plain cross join is straightforward: it is the combination of A‘s entities class and B‘s entity class. Then the primary key of the cross join should be the concatenation of the primary keys of A and B.

DataJoint provides only one kind of join: the natural join.  The join operator is further constrained to be valid only when all shared attributes are in the primary key or in a foreign key in both operands.  If the two operands share an attribute that is not part of a primary key or foreign key in either of them, DataJoint will raise an error.  As the primary key of the output, DataJoint designates the union of the primary key of the operands.  This definition follows the logic of the primary key of the cross join.

A natural join is a cross join followed by an equality restriction.  As we have already seen in the restriction discussion (Strong Entity Integrity: Part 3 — Restriction), equality restrictions involving primary key attributes can alter the true (minimal) primary key. As a result, a natural join may have one or more candidate keys that are subsets of the full primary key of the cross join.

Therefore, again, DataJoint makes a compromise for the sake of Strong Entity Integrity: It designates as the primary key the union of the primary keys of the join’s operands, supporting the idea that the entity class of a join is the combination of the entity classes of its operands. However, from the purely relational principles, we may often find a more concise candidate key whose entity class may not be well defined.

To analyze these scenarios, we make use of the notation of functional dependencies and apply Armstrong’s axioms to derive possible valid primary keys of join results.

Let ab → cd designate a relation with the primary key attributes a and b and dependent attributes c and d. The fact that ab comprise the primary key means that cd are functionally dependent on ab. When we natural join two relations, we must designate a new functional dependency that is congruent with the two original functional dependencies. DataJoint accomplishes this with the simple rule of keeping primary key attributes of the operands in the primary key of the result. In the table below, we apply Armstrong’s axioms to derive other candidate keys that may be shorter than DataJoint’s choice.

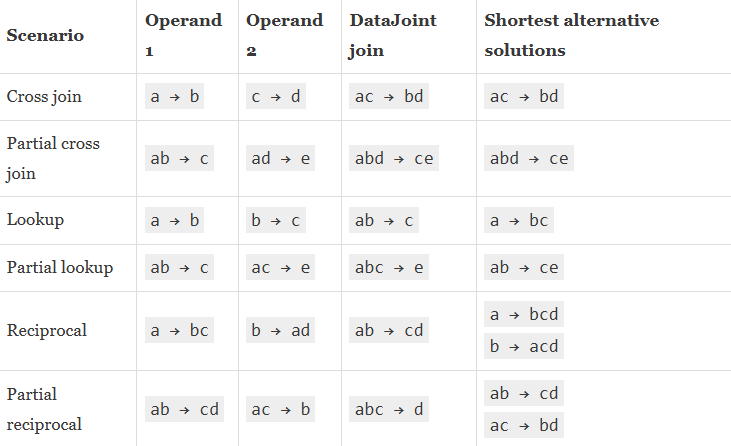
These derivations demonstrate that DataJoint often suggests a primary key that is a superset of shorter candidate keys. We justify this choice by the adherence to Strong Entity Integrity: The rules of entity identity must be simple for humans to predict and comprehend.

As an illustration, let’s consider the example of a table containing a filtered image that’s defined as follows (in Python):

@schema

class FilteredImage(dj.Computed):

   definition = """

   -> Image

   ---

   -> ImageFilter

   """

Here ImageFilter is not included in the primary key and is not part of the entity identity of FilteredImage. Therefore, there can be only one FilteredImage for each Image. This corresponds to the Lookup scenario in the table above. Then the join FilteredImage() * ImageFilter() simply appends the dependent attributes of ImageFilter to FilteredImage without altering the entity class: each entry can be fully identified by the image alone. Yet DataJoint will include the primary key of FilteredImage in the primary key of the result, maintaining the principle that the entity class of a join is any combination of the entity classes of its operands as if any join is a cross join.